правила, методы, примеры как делить квадратные корни

Наличие квадратных корней в выражении усложняет процесс деления, однако существуют правила, с помощью которых работа с дробями становится значительно проще.

Единственное, что необходимо все время держать в голове —  подкоренные выражения делятся на подкоренные выражения, а множители на множители. В процессе деления квадратных корней мы упрощаем дробь. Также, напомним, что корень может находиться в знаменателе.

Метод 1. Деление подкоренных выражений

Алгоритм действий:

Записать дробь

Если выражение не представлено в виде дроби, необходимо его так записать, потому так легче следовать принципу деления квадратных корней.

Пример 1

144÷36, это выражение следует переписать так: 14436

Использовать один знак корня

В случае если и в числителе, и знаменателе присутствует квадратные корни, необходимо записать их подкоренные выражения под одним знаком корня, чтобы сделать процесс решения проще.

Напоминаем, что подкоренным выражением (или числом) является выражением под знаком корня.

Пример 2

14436. Это выражение следует записать так: 14436

Разделить подкоренные выражения

Просто разделите одно выражение на другое, а результат запишите под знаком корня.

Пример 3

14436=4, запишем это выражение так: 14436=4

Упростить подкоренное выражение (если необходимо)

Если подкоренное выражение или один из множителей представляют собой полный квадрат, упрощайте такое выражение.

Напомним, что полным квадратом является число, которое представляет собой квадрат некоторого целого числа.

Пример 4

4 — полный квадрат, потому что 2×2=4. Из этого следует:

4=2×2=2. Поэтому 14436=4=2.

Метод 2. Разложение подкоренного выражения на множители

Алгоритм действий:

Записать дробь

Перепишите выражение в виде дроби (если оно представлено так). Это значительно облегчает процесс деления выражений с квадратными корнями, особенно при разложении на множители.  

Пример 5

8÷36, переписываем так 836

Разложить на множители каждое из подкоренных выражений

Число под корнем разложите на множители, как и любое другое целое число, только множители запишите под знаком корня.

Пример 6

Упростить числитель и знаменатель дроби

Для этого следует вынести из-под знака корня множители, представляющие собой полные квадраты. Таким образом, множитель подкоренного выражения станет множителем перед знаком корня.

Пример 7

2266×62×2×2, из этого следует: 836=226

Рационализировать знаменатель (избавиться от корня)

В математике существуют правила, по которым оставлять корень в знаменателе — признак плохого тона, т.е. нельзя. Если в знаменателе присутствует квадратный корень, то избавляйтесь от него. 

Умножьте числитель и знаменатель на квадратный корень, от которого необходимо избавиться.

Пример 8

В выражении 623 необходимо умножить числитель и знаменатель на 3, чтобы избавиться от него в знаменателе:

623×33=62×33×3=669=663

Упростить полученное выражение (если необходимо)

Если в числителе и знаменателе присутствуют числа, которые можно и нужно сократить. Упрощайте такие выражения, как и любую дробь.

Пример 9

26 упрощается до 13; таким образом 226упрощается до 123=23

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание  

Метод 3. Деление квадратных корней с множителями

Алгоритм действий:

Упростить множители

Напомним, что множители представляют собой числа, стоящие перед знаком корня. Для упрощения множителей понадобится разделить или сократить их. Подкоренные выражения не трогайте!

Пример 10

432616. Сначала сокращаем 46: делим на 2 и числитель, и знаменатель: 46=23.

Упростить квадратные корни

Если числитель нацело делится на знаменатель, то делите. Если нет, то упрощайте подкоренные выражения, как и любые другие.

Пример 11

32 делится нацело на 16, поэтому: 3216=2

Умножить упрощенные множители на упрощенные корни

Помним про правило: не оставлять в знаменателе корни. Поэтому просто перемножаем числитель и знаменатель на этот корень.

Пример 12

Рационализировать знаменатель (избавиться от корня в знаменателе)

Пример 13

4327. Следует умножить числитель и знаменатель на 7, чтобы избавиться от корня в знаменателе.

437×77=43×77×7=42149=4217

Метод 4. Деление на двучлен с квадратным корнем

Алгоритм действий:

Определить, находится ли двучлен (бином) в знаменателе

Напомним, что двучлен представляет собой выражение, которое включает 2 одночлена. Такой метод имеет место быть только в случаях, когда в знаменателе двучлен с квадратным корнем.

Пример 14

15+2— в знаменателе присутствует бином, поскольку есть два одночлена.

Найти выражение, сопряженное биному

Напомним, что сопряженный бином является двучленом с теми же одночленами, но с противоположными знаками. Чтобы упростить выражение и избавиться от корня в знаменателе, следует перемножить сопряженные биномы.

Пример 15

5+2и 5-2 — сопряженные биномы.

Умножить числитель и знаменатель на двучлен, который сопряжен биному в знаменателе

Такая опция поможет избавиться от корня в знаменателе, поскольку произведение сопряженных двучленов равняется разности квадратов каждого члена биномов: (a-b)(a+b)=a2-b2

Пример 16

15+2=1(5-2)(5-2)(5+2)=5-2(52-(2)2=5-225-2=5-223.

Из этого следует: 15+2=5-223.

Советы: 

1. Если вы  работаете с квадратными корнями смешанных чисел, то преобразовывайте их в неправильную дробь. 
2. Отличие сложения и вычитания от деления — подкоренные выражения в случае деления не рекомендуется упрощать (за счет полных квадратов).
3. Никогда (!) не оставляйте корень в знаменателе.
4. Никаких десятичных дробей или смешанных перед корнем — необходимо преобразовать их в обыкновенную дробь, а потом упростить.
5. В знаменателе сумма или разность двух одночленов? Умножьте такой бином на сопряженный ему двучлен и избавьтесь от корня в знаменателе.

Действия с корнями.

1. Главная
2. Алгебра
3. Степени и корни
4. Действия с корнями.

Умножение корней с одинаковыми показателями

Чтобы перемножить корни с одинаковыми показателями, нужно оставить тот же показатель корня, а подкоренные выражения перемножить.

√(81) × √(25) =
= √(81 × 25) =
= 9 × 5 =
= 45

Умножение корней с разными показателями

Чтобы перемножить корни с разными показателями, нужно сначала привести корни к общему показателю, а потом перемножить полученные корни с одинаковым показателем. Чтобы умножить корень на число, надо занести под знак корня это число, возведённое в степень с показателем, как у корня.

∛‎(729) × √(25) =
= √(81) × √(25) =
= √(81 × 25) =

= 9 × 5 =
= 45

Деление корней с одинаковыми и разными показателями

Чтобы разделить корни с одинаковыми показателями, нужно разделить подкоренные выражения, а показатель корня оставить прежний.

^√(81) / _√(25) =
= √(⁸¹ / ₂₅) =
= ⁹ / ₅

Если показатели корней разные, то сначала нужно привести корни к общему показателю, а потом — поделить получившиеся корни с одинаковыми показателями.Можно делить (число на корень или корень на число) — для этого нужно занести под знак корня (в числитель или в знаменатель) это число, возведённое в степень с показателем, как у корня.

^∛‎(729) / _√(25) =
= ^√(81) / _√(25) =
= √(⁸¹ / ₂₅) =
= ⁹ / ₅

Возведение корней в степень

Чтобы возвести корень в степень, нужно возвести в эту степень подкоренное выражение, а показатель корня оставить тем же.

(∛‎(125))² = (∛‎(125²))

Извлечение корня из корня

Чтобы извлечь корень из корня, нужно перемножить показатели корней, а подкоренное выражение оставить прежним.

Уничтожение иррациональности в знаменателе

Чтобы избавиться от иррациональности в знаменателе, нужно домножить на одно и то же выражение числитель и знаменатель дроби, пользуясь по мере надобности формулами сокращённого умножения. Если в знаменатетеле дроби корень числа — домножаем на такой же корень, и в знаменателе оказывается само число.

⁷ / _√(5) =
= ^{7 × √(5)} / ₅

Если в знаменателе дроби сумма/разность корней двух чисел — домножаем на разность/сумму этих корней, и в знаменателе оказывается разность самих чисел.

⁷ / _{[ √(7) — √(3) ]} =
= ^{7 × [ √(7) + √(3) ]} / _{[ 7 — 3 ]}

=
= ^{7 × [ √(7) + √(3) ]} / ₄

Если в знаменателе сумма/разность кубических корней двух чисел — домножаем на неполный квадрат разности/суммы этих кубических корней. В знаменателе получается сумма/разность самих чисел.Если в знаменателе неполный квадрат суммы/разности кубических корней двух чисел — домножаем на разность/сумму этих кубических корней. В знаменателе получается разность/сумма самих чисел.

⁵ / _{[ ∛(7) + ∛(4) ]} =
= ^{5 × [ ∛(49) — ∛(7 × 4) + ∛(16) ]} / _{[ 7 + 4 ]} =
= ^{5 × [ ∛(49) — ∛(7 × 4) + ∛(16) ]} / ₁₁

Как поделить корень на корень

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. »
И для тех, кто «очень даже. » )

Продолжаем развлечение? В предыдущих уроках мы осознали, что такое квадратный корень. И разобрались как умножать корни. Формулу умножения корней мы разобрали по винтикам. Очень уж она полезная в решении примеров! Осталось ещё две. Переходим к следующей формуле. Это будет

деление корней.

Формула столь же проста, как и умножение. Вот она:

Напоминаю: здесь а — неотрицательное число (больше или равно нулю), b — положительное (больше нуля)! Иначе формула смысла не имеет. Об этих тонкостях мы ниже поговорим.

У формулы деления корней возможности не так обширны, как у умножения. Что можно делать прямо по формуле? Очевидно, делить корни.

Как делить корни?

Элементарно. Вот вам примерчик:

В этом примере деление корней помогло нам получить хороший ответ. Бывают более хитрые преобразования. Например:

Здесь мы превратили двойку в корень квадратный из четырёх. Исключительно для того, чтобы формулу деления корней в дело употребить. Как видите, ничего здесь сложного нет.

Рассмотрим формулу деления корней в обратном направлении. Справа налево. Вот так:

Какие возможности раскрывает нам такая запись? Ничего нового, думаете? Ошибаетесь! Забавно, но простая запись формулы в другом направлении частенько высвечивает дополнительные возможности!

В нашем случае такая формулировка деления корней здорово помогает извлекать корни из дробей! Например, пусть нам надо извлечь квадратный корень из дроби 25/144. Спокойно пишем себе:

Вот и все дела! От работы с дробью целиком, мы переходим к работе отдельно с числителем, отдельно со знаменателем. Что гораздо проще. А если дробь десятичная? Не вопрос! Если сразу корень не можете извлечь — переводите десятичную дробь в обыкновенную, и — вперёд! По формуле деления корней. Например:

Бывает ещё круче, когда корень из смешанного числа надо извлечь! Как поступаем? Правильно! Переводим смешанное число в неправильную дробь — и по знакомой формуле деления корней! К примеру, вот так:

Что, забыли, как переводить дроби? Срочно двигайте в тему «Дроби» и вспоминайте. А то ни дробь преобразовать, ни сократить её. И зачем вам тогда квадратные корни?

Надеюсь, что деление корней проблем не составляет. Простая и безобидная формула, простое употребление. Теперь в нашем арсенале уже две формулы. Умножение и деление корней. Табурет на двух ножках. Сидеть можно, но. некомфортно.)

Займёмся последним свойством квадратных корней.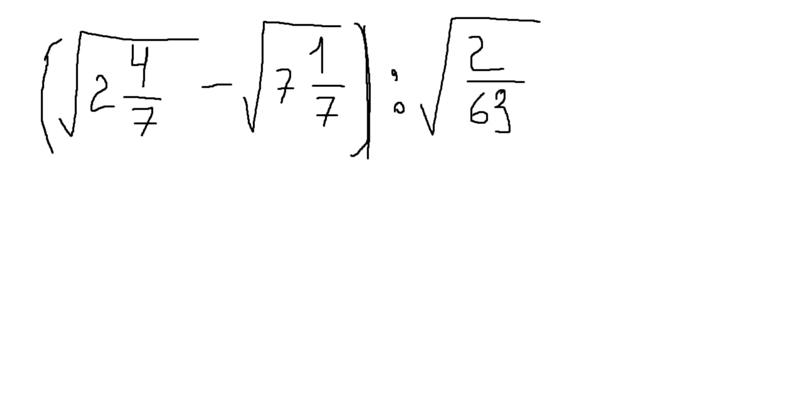 Здесь уже будут некоторые тонкости и подводные камни. Это свойство кратко называют корень из квадрата. Или корень в квадрате. Или корень из степени. Корень в степени. Всяко называют. Но суть одна. Это возведение в степень подкоренного выражения или самого корня.

Можно ли корень возвести в квадрат? А почему нет? Умножить корень сам на себя — да все дела! И не только в квадрат можно. В любую степень. А извлечь корень из квадрата? Да тоже не проблема! Мы же умеем корень из произведения извлекать. Так что можно извлечь корень не только из квадрата, но и из любой степени.

Но именно эти действия вызывают массу проблем. С этим надо разобраться основательно. Что мы сейчас и сделаем. Начнём с безобидного действия. С корня в квадрате.

Как возвести корень в квадрат?

Так как посчитать корень в квадрате? Очень просто. Прямо по смыслу корня. Что такое корень квадратный из двух, например? Это число, которое при возведении в квадрат должно дать двойку. Так вот, если мы число, которое при возведении в квадрат должно дать двойку, возведём-таки в этот самый квадрат? Что получим? Двойку, конечно! Т.е. подкоренное выражение. Или, в общем виде:

Вот и всё! Никаких подводных камней, всё строго по формуле! Возведение в квадрат корня квадратного из любого выражения даст нам это самое выражение. Понятно, что а — число неотрицательное. Иначе формула смысла не имеет.

А если корень не в квадрате, а в другой степени? Не вопрос! Если, конечно, знаете действия со степенями. По правилам этих действий сами приведём исходное выражение к корням в квадрате и всё посчитаем. Например, вот так (расписываю подробно):

Как видим, корень исчезает, Степень результата в два раза меньше исходной степени.

Если степень нечётная — разложим исходное выражение на множители, и все дела:

Так поступаем с любой степенью корня из любого выражения, и всё у нас посчитается, упростится и получится. Корень в квадрате — штука бесхитростная. Разберёмся теперь с корнем из квадрата.

Как извлечь корень из квадрата?

Пусть у нас есть хорошее число 2. Возведём его в квадрат.

Кто бы спорил? А теперь давайте обратно, извлечём из результата квадратный корень:

Опять всё чудесно, правда? С чего начали, к тому и вернулись! Стало быть, можно записать:

Оно и естественно, правда? Возведение в квадрат компенсируется обратной операцией — извлечением квадратного корня. В общем виде формула выглядит вот так:

Стоп! Внимание! Во всех учебниках, справочниках и пособиях рядом с такой формулой всегда пишут: «где а — больше, либо равно нулю». В этих словах, которые многие просто пропускают, и кроются главные сложности корней. Потому, что в примерах а частенько бывает отрицательным! Пока и мы будем считать, что а — неотрицательное. Для простоты. А вот как встретите на этой странице мрачного зайца — вот там и начнётся настоящая работа!

Продолжаем. Корень из квадрата извлекается просто. А если у нас подкоренное выражение не в квадрате, а в другой степени? Допустим, в четвёртой? Да нет проблем. Приведём нашу степень к квадрату. Вот так:

Для таких преобразований надо опять-таки знать действия со степенями, но тут уж ничего не поделаешь.

Теперь по формуле корня из квадрата:

Вот и всё. Корень из любой чётной степени даст в результате подкоренное выражение в степени, в два раза меньше исходной. Корень из 3 10 ? Легко! Это будет 3 5 . Корень из 5 18 ? Запросто! Это будет 5 9 . Ну, и так далее.

А если степень нечётная? Подумаешь! Раскладываем подкоренное выражение на множители — и вперёд! Используем вынесение множителя из-под корня. Например:

Всё просто. Но до сего момента мы работали только с неотрицательными числами и выражениями. Как только в игру вступают отрицательные величины, простота куда-то пропадает начисто. Вернём эту простоту и ясное понимание.

Вот тут и будет мрачный заяц. Для лучшего запоминания.) Концентрируем внимание и собираем весь интеллект в кулак!)

Итак, откуда в корнях могут появиться отрицательные числа и выражения?

Пунктик первый. Отрицательные значения даны прямо в задании. Вспоминаем пример корня из квадрата двойки:

Здесь всё понятно и просто.

А теперь попробуем вычислить:

Берём, и просто считаем, безо всяких формул:

Извлекаем корень из четырёх и получаем 2. Так как арифметический квадратный корень (а в школе мы работаем только с такими!) — всегда число неотрицательное! То есть:

А если бы мы использовали формулу:

получили бы не два, а минус два! Что является ошибкой.

Не работает эта формула для отрицательных значений.

Для того, чтобы формула корня из квадрата работала для всех значений а, она записывается вот так:

Это и есть последнее, третье свойство корней. Корень из квадрата. Третья ножка для табурета.)

Здесь появляется страшный значок для старшеклассников. Модуль. Если вы пока не сильны в раскрытии модулей, не волнуйтесь. Здесь он означает лишь то, что при любом знаке а, результат извлечения корня из квадрата будет всегда неотрицательный. Формула стала полноценной. Модуль просто отсекает минусы:

Пунктик второй. Отрицательные значения спрятаны в буквах и дополнительных условиях. Например, требуется упростить выражение:

Не выходит? Смотрим ЗАКЛЮЧЕНИЕ урока.

Получилось? Неплохо. А как вам эти примерчики?

Вычислить (все буквы — неотрицательные):

Ответы (в беспорядке): выражение не имеет смысла; 5; 4; 1; -3; 0,5

Всё нормально!? Отлично. Корни — не ваша проблема.

Не всё понятно? Не беда. Читаем дальше.

Не получаются даже простые примеры? Или не очень простые? Хотелось бы увидеть решение всех примеров с подробными и понятными объяснениями? Нет проблем! Идём в Особый раздел 555. Квадратные корни. Там даны все разъяснения. Которые, между прочим, годятся не только для решения этих примеров.

Это и будет последняя, четвёртая ножка для табурета.) Которая не даст свалиться и при серьёзных заданиях.

Особо ценная информация Раздела 555 помогает даже в самых запущенных случаях!) Когда не получается — и всё тут! Не говоря уж об отдельных неясностях. В этом разделе вы познакомитесь с практической работой с корнями.

И всё получится.

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Вот здесь можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

А вот здесь можно познакомиться с функциями и производными.

Наличие квадратных корней в выражении усложняет процесс деления, однако существуют правила, с помощью которых работа с дробями становится значительно проще.

Единственное, что необходимо все время держать в голове — подкоренные выражения делятся на подкоренные выражения, а множители на множители. В процессе деления квадратных корней мы упрощаем дробь. Также, напомним, что корень может находиться в знаменателе.

Метод 1. Деление подкоренных выражений

Записать дробь

Если выражение не представлено в виде дроби, необходимо его так записать, потому так легче следовать принципу деления квадратных корней.

144 ÷ 36 , это выражение следует переписать так: 144 36

Использовать один знак корня

В случае если и в числителе, и знаменателе присутствует квадратные корни, необходимо записать их подкоренные выражения под одним знаком корня, чтобы сделать процесс решения проще.

Напоминаем, что подкоренным выражением (или числом) является выражением под знаком корня.

144 36 . Это выражение следует записать так: 144 36

Разделить подкоренные выражения

Просто разделите одно выражение на другое, а результат запишите под знаком корня.

144 36 = 4 , запишем это выражение так: 144 36 = 4

Упростить подкоренное выражение (если необходимо)

Если подкоренное выражение или один из множителей представляют собой полный квадрат, упрощайте такое выражение.

Напомним, что полным квадратом является число, которое представляет собой квадрат некоторого целого числа.

4 — полный квадрат, потому что 2 × 2 = 4 . Из этого следует:

4 = 2 × 2 = 2 . Поэтому 144 36 = 4 = 2 .

Метод 2. Разложение подкоренного выражения на множители

Записать дробь

Перепишите выражение в виде дроби (если оно представлено так). Это значительно облегчает процесс деления выражений с квадратными корнями, особенно при разложении на множители.

8 ÷ 36 , переписываем так 8 36

Разложить на множители каждое из подкоренных выражений

Число под корнем разложите на множители, как и любое другое целое число, только множители запишите под знаком корня.

8 36 = 2 × 2 × 2 6 × 6

Упростить числитель и знаменатель дроби

Для этого следует вынести из-под знака корня множители, представляющие собой полные квадраты. Таким образом, множитель подкоренного выражения станет множителем перед знаком корня.

2 2 6 6 × 6 2 × 2 × 2 , из этого следует: 8 36 = 2 2 6

Рационализировать знаменатель (избавиться от корня)

В математике существуют правила, по которым оставлять корень в знаменателе — признак плохого тона, т.е. нельзя. Если в знаменателе присутствует квадратный корень, то избавляйтесь от него.

Умножьте числитель и знаменатель на квадратный корень, от которого необходимо избавиться.

В выражении 6 2 3 необходимо умножить числитель и знаменатель на 3 , чтобы избавиться от него в знаменателе:

6 2 3 × 3 3 = 6 2 × 3 3 × 3 = 6 6 9 = 6 6 3

Упростить полученное выражение (если необходимо)

Если в числителе и знаменателе присутствуют числа, которые можно и нужно сократить. Упрощайте такие выражения, как и любую дробь.

2 6 упрощается до 1 3 ; таким образом 2 2 6 упрощается до 1 2 3 = 2 3

Метод 3. Деление квадратных корней с множителями

Упростить множители

Напомним, что множители представляют собой числа, стоящие перед знаком корня. Для упрощения множителей понадобится разделить или сократить их. Подкоренные выражения не трогайте!

4 32 6 16 . Сначала сокращаем 4 6 : делим на 2 и числитель, и знаменатель: 4 6 = 2 3 .

Упростить квадратные корни

Если числитель нацело делится на знаменатель, то делите. Если нет, то упрощайте подкоренные выражения, как и любые другие.

32 делится нацело на 16 , поэтому: 32 16 = 2

Умножить упрощенные множители на упрощенные корни

Помним про правило: не оставлять в знаменателе корни. Поэтому просто перемножаем числитель и знаменатель на этот корень.

Рационализировать знаменатель (избавиться от корня в знаменателе)

4 3 2 7 . Следует умножить числитель и знаменатель на 7 , чтобы избавиться от корня в знаменателе.

4 3 7 × 7 7 = 4 3 × 7 7 × 7 = 4 21 49 = 4 21 7

Метод 4. Деление на двучлен с квадратным корнем

Определить, находится ли двучлен (бином) в знаменателе

Напомним, что двучлен представляет собой выражение, которое включает 2 одночлена. Такой метод имеет место быть только в случаях, когда в знаменателе двучлен с квадратным корнем.

1 5 + 2 — в знаменателе присутствует бином, поскольку есть два одночлена.

Найти выражение, сопряженное биному

Напомним, что сопряженный бином является двучленом с теми же одночленами, но с противоположными знаками. Чтобы упростить выражение и избавиться от корня в знаменателе, следует перемножить сопряженные биномы.

5 + 2 и 5 — 2 — сопряженные биномы.

Умножить числитель и знаменатель на двучлен, который сопряжен биному в знаменателе

Такая опция поможет избавиться от корня в знаменателе, поскольку произведение сопряженных двучленов равняется разности квадратов каждого члена биномов: ( a — b ) ( a + b ) = a 2 — b 2

1 5 + 2 = 1 ( 5 — 2 ) ( 5 — 2 ) ( 5 + 2 ) = 5 — 2 ( 5 2 — ( 2 ) 2 = 5 — 2 25 — 2 = 5 — 2 23 .

Из этого следует: 1 5 + 2 = 5 — 2 23 .

Советы:

1. Если вы работаете с квадратными корнями смешанных чисел, то преобразовывайте их в неправильную дробь.
2. Отличие сложения и вычитания от деления — подкоренные выражения в случае деления не рекомендуется упрощать (за счет полных квадратов).
3. Никогда (!) не оставляйте корень в знаменателе.
4. Никаких десятичных дробей или смешанных перед корнем — необходимо преобразовать их в обыкновенную дробь, а потом упростить.
5. В знаменателе сумма или разность двух одночленов? Умножьте такой бином на сопряженный ему двучлен и избавьтесь от корня в знаменателе.

А извлечь корень из квадрата? Множитель – число, стоящее непосредственно перед знаком корня. Так, например, в выражении 2(квадратный корень)5, число 5 является подкоренным выражением, а число 2 — множителем. Собственно, это и есть главная трудность в работе с корнями.

Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Перемножьте все члены между собой, включая множители перед корнями и подкоренные выражения. Всегда ищите делитель, из которого можно взять целый корень; это облегчит процесс. Если вы хотите узнать, как умножить корни с или без множителей, прочитайте эту статью.

Метод 1 из 3: Умножение корней без множителей

Перемножьте числа под корнем. Запишите каждый корень с НОК в качестве нового показателя. Знак корня является еще одним способом записи дробных показателей. Когда множитель и корень записаны рядом, то это означает их умножение: 2*(квадратный корень)5. В предыдущих уроках мы осознали, что такое квадратный корень. И разобрались как умножать корни. Формулу умножения корней мы разобрали по винтикам.

Метод 3 из 3: Перемножение двучленов с квадратными корнями

Формула столь же проста, как и умножение. У формулы деления корней возможности не так обширны, как у умножения. В этом примере деление корней помогло нам получить хороший ответ. Бывают более хитрые преобразования.

Исключительно для того, чтобы формулу деления корней в дело употребить. В нашем случае такая формулировка деления корней здорово помогает извлекать корни из дробей! Не вопрос! Если сразу корень не можете извлечь — переводите десятичную дробь в обыкновенную, и — вперёд! Бывает ещё круче, когда корень из смешанного числа надо извлечь! Правильно! Переводим смешанное число в неправильную дробь — и по знакомой формуле деления корней!

Как делить корни?

Надеюсь, что деление корней проблем не составляет. Займёмся последним свойством квадратных корней. Здесь уже будут некоторые тонкости и подводные камни. Это свойство кратко называют корень из квадрата. Мы же умеем корень из произведения извлекать. Это число, которое при возведении в квадрат должно дать двойку. Возведение в квадрат корня квадратного из любого выражения даст нам это самое выражение.

По правилам этих действий сами приведём исходное выражение к корням в квадрате и всё посчитаем. Так поступаем с любой степенью корня из любого выражения, и всё у нас посчитается, упростится и получится. Пусть у нас есть хорошее число 2. Возведём его в квадрат. Во всех учебниках, справочниках и пособиях рядом с такой формулой всегда пишут: «где а — больше, либо равно нулю». В этих словах, которые многие просто пропускают, и кроются главные сложности корней.

Продолжаем. Корень из квадрата извлекается просто. А если у нас подкоренное выражение не в квадрате, а в другой степени? Извлекаем корень из четырёх и получаем 2. Так как арифметический квадратный корень (а в школе мы работаем только с такими!) — всегда число неотрицательное! Это и есть последнее, третье свойство корней.

Здесь он означает лишь то, что при любом знаке а, результат извлечения корня из квадрата будет всегда неотрицательный. Если х Глазки у ребенка начали гноится когда мы были еще в роддоме. Тогда мы даже попали в больницу. С 1996г. по 2004г. работал детским […]

Красные пятна на листьях смородины Махровость черной смородины. Листья скручиваются и преждевременно опадают. Листовые пилильщики повреждают красную и белую смородину, […]

Ветрянка у детей Основные симптомы ветрянки у детей — это красная, зудящая сыпь, которая чем-то напоминает последствия укусов насекомых. Но это не значит, […]

Как правильно делить корни растений

     Деление корней цветов просто необходимо, если вы решили сразу за одно «мероприятие» получить пару сильных и взрослых растений, которые в будущем будут готовы к цветению. Но если рассматривать этот вопрос с иной стороны, то можно сказать, что деление корней может негативно сказаться на состоянии растений, особенно при неправильной работе с корнями.

     Прежде чем разбирать вопрос – как делить корни, необходимо определиться с растениями, которые можно так размножать. Прежде всего, это травянистые экземпляры с хорошей корневой системой. Делить таким образом можно цветы и кустарники.

Алгоритм деления корней:

1. Цветок извлеките из грунта и стряхните большой ком земли.

2. Остатки почвы смойте водой, но не нужно полностью очищать корни, главное, чтобы почва не мешала вам при делении.

3. Оцените корневую систему, и решите, сколько взрослых цветов может получиться из этого одного экземпляра. Внимание обращайте на побеги и почки.

4. Осуществите обрезку побегов на высоту 10 см. Это мероприятие поможет использовать силы цветов для восстановления корней, а не роста побегов.

5. Если корневые отростки начали твердеть, и видно, что ничего хорошего с них не получиться, то эти корни срезают.

6. Желтые и сухие побеги, листья сразу уничтожают.

7. Обратите внимание на то, что центральная часть цветка делиться не должна. Вы отделяете лишь боковые корни.

8. Срезы обрабатывают древесным углем, а новые растения высаживают в специальные горшки.

Что вы еще должны знать о делении корней

      Не выполняйте этот процесс во время цветения растения. Лучше проводить его после этого периода. Если соблюсти эту рекомендацию сложно, то за пару дней перед процессом бутоны и цветы уничтожают, иначе цветок прижиться не сможет.

      Кустарник в открытой почве разделяют осенью, а комнатные цветы – весной. Перед извлечением растения из земли, грунт хорошо поливают, чтобы корневая система не повредилась. Ни в коем случае не тяните растение за наземную часть. Корневую систему вынимают вместе с грунтом, стуча по горшку. Если цветок растет на клумбе, то его осторожно подкапывают и достают при помощи садовых инструментов. Для минимального повреждения корневой системы используют острый нож. Корневую систему не ломайте руками! Это негативно скажется на состоянии будущего цветка.

Обратите внимание! Не делите куст на маленькие части, так как это может негативно сказаться на их росте и развитии. Приживаемость будет минимальной. Не забывайте, что на каждой части должны быть один взрослый побег.

      В открытую почву сразу высаживать растения нельзя, так как им нужен период восстановления, да и лучи солнца на растения повлияют негативно.

Польза размножения делением куста

     Кроме того, что растений становится больше, они еще и омолаживаются. Ведь спорить бессмысленно с тем, что биологический возраст всех живых существ не вечен, и растение не стало исключением.2=400\\ \hline \end{array}\]

Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\] Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\), то первоначально вы должны найти значения \(\sqrt{25}\) и \(\sqrt{49}\), а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\) или \(\sqrt b\) при сложении \(\sqrt a+\sqrt b\) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt 2+ \sqrt {49}\) мы можем найти \(\sqrt{49}\) – это \(7\), а вот \(\sqrt 2\) никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt 2+7\). Дальше это выражение, к сожалению, упростить никак нельзя   \(\bullet\) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad \sqrt a:\sqrt b=\sqrt{a:b}\] (при условии, что обе части равенств имеют смысл)
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot 2}=\sqrt{64}=8\);   \(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\);   \(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}= 5\cdot 8=40\).   \(\bullet\) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\). Так как \(44100:100=441\), то \(44100=100\cdot 441\). По признаку делимости число \(441\) делится на \(9\) (так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\), то есть \(441=9\cdot 49\).
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}= \sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}= \sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{ \dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot \sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\) Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\) (сокращенная запись от выражения \(5\cdot \sqrt2\)). Так как \(5=\sqrt{25}\), то \[5\sqrt2=\sqrt{25}\cdot \sqrt2=\sqrt{25\cdot 2}=\sqrt{50}\] Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\),
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\).2\), поэтому \(\sqrt{16}=4\). А вот извлечь корень из числа \(3\), то есть найти \(\sqrt3\), нельзя, потому что нет такого числа, которое в квадрате даст \(3\).
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\) и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\)), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\)) и т.д.
\(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.  

Факт 5.
\(\bullet\) Модуль вещественного числа \(a\) – это неотрицательное число \(|a|\), равное расстоянию от точки \(a\) до \(0\) на вещественной прямой.2\\ &2>2,25 \end{aligned}\] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1<0,5\).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3<\sqrt2\) нельзя (убедитесь в этом сами)!   \(\bullet\) Следует запомнить, что \[\begin{aligned} &\sqrt 2\approx 1,4\\[1ex] &\sqrt 3\approx 1,7 \end{aligned}\] Знание приблизительного значения данных чисел поможет вам при сравнении чисел!   \(\bullet\) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа.2=168\cdot 168=28224\).
Следовательно, \(\sqrt{28224}=168\). Вуаля!

1 корень из 3 делить на 3

Вы искали 1 корень из 3 делить на 3? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 3 делить на корень из 3, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 корень из 3 делить на 3».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 1 корень из 3 делить на 3,3 делить на корень из 3,корень 3 делить на 3,корень из 3 деленное на 3,корень из 3 делить на 3. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 1 корень из 3 делить на 3. Просто введите задачу в окошко и нажмите «решить» здесь (например, корень 3 делить на 3).

Где можно решить любую задачу по математике, а так же 1 корень из 3 делить на 3 Онлайн?

Решить задачу 1 корень из 3 делить на 3 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Умножение корней

19 января 2017

Приветствую, котаны! В прошлый раз мы подробно разобрали, что такое корни (если не помните, рекомендую почитать). Главный вывод того урока: существует лишь одно универсальное определение корней, которое вам и нужно знать. Остальное — брехня и пустая трата времени.

Сегодня мы идём дальше. Будем учиться умножать корни, изучим некоторые проблемы, связанные с умножением (если эти проблемы не решить, то на экзамене они могут стать фатальными) и как следует потренируемся. Поэтому запасайтесь попкорном, устраивайтесь поудобнее — и мы начинаем.:)

Вы ведь тоже ещё не вкурили?

Урок получился довольно большим, поэтому я разделил его на две части:

1. Сначала мы разберём правила умножения. Кэп как бы намекает: это когда есть два корня, между ними стоит знак «умножить» — и мы хотим что-то с этим сделать.
2. Затем разберём обратную ситуацию: есть один большой корень, а нам приспичило представить его в виде произведения двух корней попроще. С какого перепугу это бывает нужно — вопрос отдельный. Мы разберём лишь алгоритм.

Тем, кому не терпится сразу перейти ко второй части — милости прошу. С остальными начнём по порядку.

Основное правило умножения

Начнём с самого простого — классических квадратных корней. Тех самых, которые обозначаются $\sqrt{a}$ и $\sqrt{b}$. Для них всё вообще очевидно:

Правило умножения. Чтобы умножить один квадратный корень на другой, нужно просто перемножить их подкоренные выражения, а результат записать под общим радикалом:

\[\sqrt{a}\cdot \sqrt{b}=\sqrt{a\cdot b}\]

Никаких дополнительных ограничений на числа, стоящие справа или слева, не накладывается: если корни-множители существуют, то и произведение тоже существует.

Примеры. Рассмотрим сразу четыре примера с числами:

\[\begin{align} & \sqrt{25}\cdot \sqrt{4}=\sqrt{25\cdot 4}=\sqrt{100}=10; \\ & \sqrt{32}\cdot \sqrt{2}=\sqrt{32\cdot 2}=\sqrt{64}=8; \\ & \sqrt{54}\cdot \sqrt{6}=\sqrt{54\cdot 6}=\sqrt{324}=18; \\ & \sqrt{\frac{3}{17}}\cdot \sqrt{\frac{17}{27}}=\sqrt{\frac{3}{17}\cdot \frac{17}{27}}=\sqrt{\frac{1}{9}}=\frac{1}{3}. \\ \end{align}\]

Как видите, основной смысл этого правила — упрощение иррациональных выражений. И если в первом примере мы бы и сами извлекли корни из 25 и 4 без всяких новых правил, то дальше начинается жесть: $\sqrt{32}$ и $\sqrt{2}$ сами по себе не считаются, но их произведение оказывается точным квадратом, поэтому корень из него равен рациональному числу.

Отдельно хотел бы отметить последнюю строчку. Там оба подкоренных выражения представляют собой дроби. Благодаря произведению многие множители сокращаются, а всё выражение превращается в адекватное число.

Конечно, не всегда всё будет так красиво. Иногда под корнями будет стоять полная лажа — непонятно, что с ней делать и как преобразовывать после умножения. Чуть позже, когда начнёте изучать иррациональные уравнения и неравенства, там вообще будут всякие переменные и функции. И очень часто составители задач как раз и рассчитывают на то, что вы обнаружите какие-то сокращающиеся слагаемые или множители, после чего задача многократно упростится.

Кроме того, совсем необязательно перемножать именно два корня. Можно умножить сразу три, четыре — да хоть десять! Правило от этого не поменяется. Взгляните:

Примеры.

\[\begin{align} & \sqrt{2}\cdot \sqrt{3}\cdot \sqrt{6}=\sqrt{2\cdot 3\cdot 6}=\sqrt{36}=6; \\ & \sqrt{5}\cdot \sqrt{2}\cdot \sqrt{0,001}=\sqrt{5\cdot 2\cdot 0,001}= \\ & =\sqrt{10\cdot \frac{1}{1000}}=\sqrt{\frac{1}{100}}=\frac{1}{10}. \\ \end{align}\]

И опять небольшое замечание по второму примеру. Как видите, в третьем множителе под корнем стоит десятичная дробь — в процессе вычислений мы заменяем её обычной, после чего всё легко сокращается. Так вот: очень рекомендую избавляться от десятичных дробей в любых иррациональных выражениях (т.е. содержащих хотя бы один значок радикала). В будущем это сэкономит вам кучу времени и нервов.

Но это было лирическое отступление. Теперь рассмотрим более общий случай — когда в показателе корня стоит произвольное число $n$, а не только «классическая» двойка.{2n}}}=\left| a \right|. \\ \end{align}\]

Подобные «махинации» могут здорово сэкономить вам время на экзамене или контрольной работе, поэтому запомните:

Не спешите перемножать числа в подкоренном выражении. Сначала проверьте: вдруг там «зашифрована» точная степень какого-либо выражения?

При всей очевидности этого замечания должен признать, что большинство неподготовленных учеников в упор не видят точные степени. Вместо этого они перемножают всё напролом, а затем удивляются: почему это получились такие зверские числа?:)

Впрочем, всё это детский лепет по сравнению с тем, что мы изучим сейчас.

Умножение корней с разными показателями

Ну хорошо, теперь мы умеем перемножать корни с одинаковыми показателями. А что, если показатели разные? Скажем, как умножить обычный $\sqrt{2}$ на какую-нибудь хрень типа $\sqrt[7]{23}$? Можно ли вообще это делать?

Да конечно можно. Всё делается вот по этой формуле:

Правило умножения корней.{2}}}=\sqrt[3]{5}. \\ \end{align}\]

Но тогда получается какая-то хрень:

\[\sqrt[3]{-5}=\sqrt[3]{5}\]

Этого не может быть, потому что $\sqrt[3]{-5} \lt 0$, а $\sqrt[3]{5} \gt 0$. Значит, для чётных степеней и отрицательных чисел наша формула уже не работает. После чего у нас есть два варианта:

1. Убиться об стену констатировать, что математика — это дурацкая наука, где «есть какие-то правила, но это неточно»;
2. Ввести дополнительные ограничения, при которых формула станет рабочей на 100%.

В первом варианте нам придётся постоянно вылавливать «неработающие» случаи — это трудно, долго и вообще фу. Поэтому математики предпочли второй вариант.:)

Но не переживайте! На практике это ограничение никак не влияет на вычисления, потому что все описанные проблемы касаются лишь корней нечётной степени, а из них можно выносить минусы.

Поэтому сформулируем ещё одно правило, которое распространяется вообще на все действия с корнями:

Прежде чем перемножать корни, сделайте так, чтобы подкоренные выражения были неотрицательны.{2}}}=\sqrt[4]{75}. \end{align}\]

Ну что ж, с умножением корней разобрались. Теперь рассмотрим обратную операцию: что делать, когда под корнем стоит произведение?

Смотрите также:

1. Свойства арифметического квадратного корня
2. Корень степени N
3. Пробный ЕГЭ 2012. Вариант 2 (без логарифмов)
4. Что такое ЕГЭ по математике 2012
5. Наибольшее и наименьшее значение
6. Задача 7: касательная к графику функции — 2

Как разделить квадратный корень

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Как разделить квадратный корень

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Учебное пособие по делению квадратного корня с примерами, практическими задачами и бесплатный рабочий лист с ключом ответа

Пополнение словарного запаса

Подкрепленное выражение относится к числу под знаком корня.В нижнем радикале подкоренное выражение — это цифра «5».

Еще раз о важном правиле деления квадратных корней:

Правило, описанное ниже, является важной частью того, как мы собираемся делить квадратные корни, поэтому убедитесь, что у вас есть секунда, чтобы освежить его в памяти. (Или учите впервые;)

Когда вы делите два квадратных корня, вы можете «поместить» числитель и знаменатель в один и тот же квадратный корень.Ниже приведен пример этого правила с использованием чисел

.

Как видите, «23» и «2» можно переписать внутри одного радикального знака.

Видео о том, как разделить квадратные корни

Примеры деления квадратного корня

Пример 1 умножения квадратного корня

Шаг 1

Объединить квадратные корни под 1 подкоренное число

Шаг 2

Разделить (если возможно).Так как 150 делится на 2, мы можем это сделать.

Шаг 3

Практика Деление квадратного корня

Направление: Разделите квадратные корни и выразите свой ответ в простейшей радикальной форме

Проблема 1

Показать ответ

Эта проблема похожа на пример 1.

Шаг 1

Объединить квадратные корни под 1 подкоренное число

шаг 1 ответ Шаг 2

Разделить (если возможно).Так как 200 делится на 10, мы можем это сделать.

шаг 1 ответ Шаг 3 шаг 1 ответ

Проблема 2

Показать ответ

Эта проблема похожа на пример 1

Шаг 1

Объединить квадратные корни под 1 подкоренное число

шаг 1 ответ Шаг 2

Разделить (если возможно).Поскольку 140 делится на 5, мы можем это сделать.

шаг 1 ответ Шаг 3 шаг 1 ответ

разделить квадратные корни — элементарная алгебра

Цели обучения

К концу этого раздела вы сможете:

• Разделить квадратные корни
• Рационализировать одночленный знаменатель
• Рационализировать двухчленный знаменатель

Прежде чем начать, пройдите тест на готовность.

1. Найдите дробь, эквивалентную со знаминателем 48.
   Если вы пропустили эту задачу, просмотрите (рисунок).
2. Упростить:.
   Если вы пропустили эту проблему, просмотрите (рисунок).
3. Умножить:.
   Если вы пропустили эту проблему, просмотрите (рисунок).

Разделить квадратные корни

Мы знаем, что упрощаем дроби, удаляя множители, общие для числителя и знаменателя. Когда у нас есть дробь с квадратным корнем в числителе, мы сначала упрощаем квадратный корень.Тогда мы можем искать общие факторы.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Мы использовали частное свойство квадратного корня, чтобы упростить квадратный корень из дробей. Частное свойство квадратного корня говорит о

.

Иногда нам нужно использовать частное свойство квадратного корня «в обратном порядке», чтобы упростить дробь с квадратным корнем.

Мы перепишем факторное свойство квадратного корня, чтобы мы видели оба пути вместе. Помните: мы предполагаем, что все переменные больше или равны нулю, поэтому их квадратные корни являются действительными числами.

Фактор квадратного корня

Если a , b — неотрицательные действительные числа и, тогда

Мы будем использовать частное свойство квадратных корней «в обратном порядке», когда дробь, с которой мы начинаем, является частным двух квадратных корней, и ни одно из корневых выражений не является полным квадратом.Когда мы записываем дробь в виде одного квадратного корня, мы можем найти общие множители в числителе и знаменателе.

Упростить:.

Решение

Упростить:.

Упростить:.

Мы будем использовать свойство Quotient для экспонентов, когда у нас есть переменные с показателями в подкоренных выражениях.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Упростить:.

Решение

Упростить:.

Упростить:.

Рационализация одночленного знаменателя

До того, как калькулятор стал инструментом повседневной жизни, таблицы квадратных корней использовались для нахождения приблизительных значений квадратных корней.(Рисунок) показывает часть таблицы квадратов и квадратных корней. В этой таблице квадратные корни округлены до пяти десятичных знаков.

Таблица квадратных корней использовалась для нахождения приблизительных значений квадратных корней до появления калькуляторов.

Если кому-то нужно было аппроксимировать дробь квадратным корнем в знаменателе, это означало деление в столбик с пятизначным делителем. Это был очень обременительный процесс.

По этой причине был разработан процесс, называемый рационализацией знаменателя.Дробь с радикалом в знаменателе преобразуется в эквивалентную дробь, знаменатель которой является целым числом. Этот процесс все еще используется сегодня, а также полезен в других областях математики.

Рационализация знаменателя

Процесс преобразования дроби с радикалом в знаменателе в эквивалентную дробь, знаменатель которой является целым числом, называется рационализацией знаменателя.

Квадратные корни из чисел, не являющихся полными квадратами, являются иррациональными числами.Когда мы рационализируем знаменатель , мы записываем эквивалентную дробь с рациональным числом в знаменателе.

Давайте посмотрим на числовой пример.

Но мы можем найти дробь, эквивалентную умножению числителя и знаменателя на.

Теперь, если нам нужно приблизительное значение, делим. Это намного проще.

Несмотря на то, что калькуляторы доступны почти повсюду, дробь с радикалом в знаменателе все же требует рационализации.Он не считается упрощенным, если знаменатель содержит квадратный корень.

Точно так же квадратный корень не считается упрощенным, если подкоренное выражение содержит дробь.

Упрощенный квадратный корень

Квадратный корень считается упрощенным, если имеется

• без факторов полного квадрата в подкоренном выражении
• без дробей в подкоренном остатке
• нет квадратных корней в знаменателе дроби

Чтобы рационализировать знаменатель, мы используем свойство that.Если возвести иррациональный квадратный корень в квадрат, мы получим рациональное число.

Мы будем использовать это свойство, чтобы рационализировать знаменатель в следующем примере.

Упростить:.

Решение

Чтобы рационализировать знаменатель, мы можем умножить квадратный корень сам на себя. Чтобы дробь оставалась эквивалентной, мы умножаем числитель и знаменатель на один и тот же множитель.

Упростить:.

Упростить:.

Упростить:.

Решение

Чтобы удалить квадратный корень из знаменателя, мы умножаем его на себя. Чтобы дроби оставались эквивалентными, мы умножаем числитель и знаменатель на.

Упростить:.

Упростить:.

Всегда сначала упрощайте радикал в знаменателе, прежде чем рационализировать его. Таким образом, числа остаются меньшими, и с ними легче работать.

Упростить:.

Упростить:.

Упростить:.

Упростить:.

Упростить:.

Упростить:.

Рационализировать двухчленный знаменатель

Когда знаменатель дроби представляет собой сумму или разность с квадратными корнями, мы используем паттерн Произведение конъюгатов, чтобы рационализировать знаменатель.

Когда мы умножаем бином, содержащий квадратный корень, на его сопряжение, произведение не имеет квадратных корней.

Упростить:.

Упростить:.

Упростить:.

Упростить:.

Упростить:.

Упростить:.

Упростить:.

Упростить:.

Упростить:.

Упростить:.

Ключевые понятия

• Фактор квадратного корня
  • Если a , b — неотрицательные действительные числа и, тогда
• Упрощенные квадратные корни
  Квадратный корень считается упрощенным, если есть
  • нет абсолютных квадратных множителей в подкоренном выражении
  • без дробей в подкоренном остатке
  • нет квадратных корней в знаменателе дроби

Практика ведет к совершенству

Разделить квадратные корни

Упростите следующие упражнения.

ⓐⓑ

Рационализация однозначного знаменателя

В следующих упражнениях упростите и рационализируйте знаменатель.

Рационализировать двухчленный знаменатель

В следующих упражнениях упростите, рационализируя знаменатель.

ⓐⓑ

ⓐⓑ

Повседневная математика

Комплект снабжения падает с самолета, летящего на высоте 250 футов.Упростите, чтобы определить, сколько секунд требуется комплекту снабжения, чтобы достичь земли.

Ракета сбрасывается в океан с самолета, летящего на высоте 1200 футов. Упростите, чтобы определить, сколько секунд требуется, чтобы ракета достигла океана.

Письменные упражнения

ⓐ Упростите и объясните все свои шаги.
ⓑ Упростите и объясните все свои шаги.
ⓒ Почему два метода упрощения квадратного корня различаются?

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

ⓑ После просмотра контрольного списка, думаете ли вы, что хорошо подготовились к следующему разделу? Почему или почему нет?

Глоссарий

рационализация знаменателя

Процесс преобразования дроби с радикалом в знаменателе в эквивалентную дробь, знаменатель которой является целым числом, называется рационализацией знаменателя.

Квадраты и квадратные корни Division

Эти квадратные корни хороши и все такое, но было бы лучше, если бы мы могли превратить их в дроби поверх них.Как будто мы можем читать твои мысли, верно? Пугающий.

Чтобы разделить корни, мы разделяем подкоренные выражения.

Пример задачи

Вот почему это имеет смысл: если мы умножим само на себя, мы найдем. В результате получается квадратный корень из. Возможно, вы уже знали об этом. Вероятно, это было на твоих обоях «дивизии радикалов», когда ты рос.

То же самое с переменными. Если x и y — любые неотрицательные числа (чтобы мы могли извлечь их квадратные корни), то:

Примеры задач

Разделить, если возможно, упростить:

1. 
   
2. 
   

Правило деления на радикалы можно использовать и в обратном порядке.Перед тем, как начать движение задним ходом, проверьте зеркало заднего вида. Вы не хотите перебирать какие-либо переменные. Или делать у вас?

Это правило можно использовать, чтобы разбить выражение с дробным подкоренным выражением на частное от радикалов с более красивыми подкоренными элементами. Если x и y являются неотрицательными целыми числами, то:

Пример задачи

Упростите.

Это оба числа из нашего списка, так что сразу можем сказать, что это не будет слишком болезненно.Нам нужно иметь возможность обрабатывать каждое из этих чисел отдельно, поэтому мы перепишем это выражение как частное от радикалов и упростим оттуда.

Иногда более полезно переписать квадратный корень из дроби как долю квадратных корней, как в предыдущем примере. Иногда, однако, более эффективно выполнять деление на подкоренное выражение. Мы хотели бы сказать вам, что это было более шаблонно, чем это, но вам нужно будет использовать свое собственное суждение. Наденьте черный халат и напудренный парик, если считаете, что это поможет.

Пример задачи

Упростить.

Превращение этого в частное радикалов дает.

Поскольку 28 = 4 × 7, давайте перепишем все это целиком:

Однако, если бы мы сначала сделали деление в подкоренном и, мы бы получили:

Что ж, это было намного проще. Мы поддерживаем этот метод; а ты?

Какой метод мы используем, когда? В общем, если подкоренное выражение — это дробь, которую можно упростить до полного квадрата или другого красивого, четного числа (например, целое число, умноженное на полный квадрат), сначала упростите подкоренное выражение.Если подкоренное выражение представляет собой дробь, которая не упрощается ни до чего, что нам нравится, вероятно, пора разделить выражение на частное из квадратных корней. В любом случае правильное упрощение даст нам правильный ответ. Если время от времени мы будем проделывать долгий путь, пусть будет так. По крайней мере, по пути мы можем любоваться пейзажем.

Как разделить радикалы | Sciencing

Обновлено 20 ноября 2020 г.

Крис Дезил

В математике радикал — это любое число, которое включает знак корня (√).Число под знаком корня является квадратным корнем, если перед знаком корня нет верхнего индекса, кубический корень — это верхний индекс 3 перед ним ( ³ √), корень четвертой степени, если ему предшествует 4 ( ⁴ √) и т. на. Многие радикалы нельзя упростить, поэтому деление на один требует специальных алгебраических методов. Чтобы использовать их, запомните эти алгебраические равенства:

\ sqrt {\ frac {a} {b}} = \ frac {\ sqrt {a}} {\ sqrt {b}}

\ sqrt {a × b } = \ sqrt {a} × \ sqrt {b}

Числовой квадратный корень в знаменателе

В общем, выражение с числовым квадратным корнем в знаменателе выглядит следующим образом:

\ frac {a} { \ sqrt {b}}

Чтобы упростить эту дробь, вы рационализируете знаменатель, умножив всю дробь на √ b / √ b .2} = b

\ frac {a \ sqrt {b}} {b}

1. Рационализируйте знаменатель дроби

\ frac {5} {\ sqrt {6}}

Решение: Умножьте дробь на √6 / √6

\ frac {5 \ sqrt {6}} {\ sqrt {6} \ sqrt {6}} \\ \, \\ \ frac {5 \ sqrt {6}} {6} \ text {или} \ frac {5} {6} × \ sqrt {6}

\ frac {6 \ sqrt {32}} {3 \ sqrt {8}}

Решение: В этом случае вы можете упростить, разделив числа вне знака корня и числа внутри него двумя отдельными операциями:

\ frac {6} {3} = 2 \\ \, \\ \ frac {\ sqrt {32} } {\ sqrt {8}} = \ sqrt {4} = 2

Выражение сводится к

2 × 2 = 4

Деление на кубические корни

Та же общая процедура применяется, когда радикал в знаменателе куб, корень четвертой или более высокой степени.2}}

\ frac {5} {\ sqrt [3] {5}}

Умножьте числитель и знаменатель на ³ √25.

\ frac {5 × \ sqrt [3] {25}} {\ sqrt [3] {5} × \ sqrt [3] {25}} \\ \, \\ = \ frac {5 \ sqrt [3 ] {25}} {\ sqrt [3] {125}} \\ \, \\ = \ frac {5 \ sqrt [3] {25}} {5}

Цифры вне знака корня отменяют, а ответ:

\ sqrt [3] {25}

Переменные с двумя членами в знаменателе

Когда радикал в знаменателе включает два члена, вы обычно можете упростить его, умножив на его сопряжение.2 — 3}

Конъюгаты и деление на радикалы

Purplemath

Иногда вам нужно умножать многочленные выражения, содержащие только радикалы. Это ситуация, в которой вертикальное умножение является прекрасным подспорьем.

• Упростить

Это упражнение выглядит некрасиво, но оно вполне выполнимо, если я аккуратен и точен в своей работе.

Во-первых, я делаю умножение, используя вертикальный метод, чтобы не усложнять:

MathHelp.com

Затем я устанавливаю исходное выражение, равное последней строке из приведенного выше умножения, и завершаю вычисления, упрощая каждый член:

---

• Упростить:

Сначала делаю умножение:

А потом упрощаю:

---

Обратите внимание, в последнем примере выше, как я получил все целые числа.(Хорошо, технически это целые числа, но дело в том, что члены , а не включают какие-либо радикалы.) Я перемножил два радикальных бинома и получил ответ, который не содержал радикалов. Вы также могли заметить, что два «бинома» были одинаковыми, за исключением знака посередине: у одного был «плюс», а у другого — «минус».

Эта пара факторов, где второй фактор отличается только одним знаком посередине, очень важна; на самом деле этот «тот же, за исключением знака в середине» второй множитель имеет собственное название:

Учитывая радикальное выражение

, «сопряженный» является выражением.

Конъюгат (KAHN-juh-ghitt) имеет те же числа, но с противоположным знаком посередине. Таким образом,

является не только конъюгатом, но и конъюгатом.

Кроме того, конъюгаты не обязательно должны быть двухчленными выражениями с радикалами в каждом из терминов. Фактически, любое двухчленное выражение может иметь конъюгат:

1 + sqrt [2] является конъюгатом 1 — sqrt [2] sqrt [7] — 5 sqrt [6] является конъюгатом sqrt [7] + 5 sqrt [6] x + sqrt [y] является конъюгатом x — sqrt [y]

Чтобы создать конъюгат, все, что вам нужно сделать, это перевернуть знак посередине.Все остальное остается прежним.

---

• Что такое спряжение 3 + sqrt [5]?

В этом случае я нахожу сопряжение для выражения, в котором только один из терминов имеет радикал. Хорошо. Независимо от этого, процесс тот же; а именно я переворачиваю знак посередине. Поскольку они дали мне выражение со знаком «плюс» в середине, спряжение — это те же два термина, но с «минусом» посередине:

---

• Найдите конъюгат –7 sqrt [3] — 2

На этот раз радикал находится в первом из двух членов, и перед первым термином стоит «минус».Хорошо. Я оставлю первый «минус» в покое, потому что ничего не меняю, кроме среднего знака; Переверну второй «минус» посередине на «плюс»:

---

Когда мы умножаем конъюгаты, мы делаем нечто похожее на то, что происходит, когда мы умножаем на разность квадратов; а именно:

a ² — b ² = ( a + b ) ( a — b )

Когда мы умножаем множители a + b и a — b , средние члены « ab » сокращаются:

То же самое происходит, когда мы умножаем конъюгаты:

Мы вскоре увидим, почему это важно.Чтобы понять это, давайте сначала взглянем на дроби, в знаменателях которых есть радикалы.

---

Деление на квадратные корни

Подобно тому, как мы можем переключаться между умножением радикалов и радикалом, содержащим умножение, мы можем переключаться между делением корней и одним корнем, содержащим деление.

• Упростить:

Я могу упростить это, работая внутри, а затем извлекая квадратный корень:

…или иначе, разделив разделение на два радикала, упрощение и исключение:

В любом случае, мой окончательный ответ такой же.

---

• Упростить:

Я вижу, что в знаменателе есть полный квадрат, а в числителе — простое число.

No related posts.